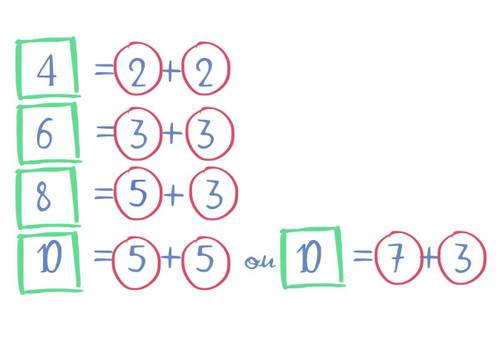Vieux problème cherche démonstration

"Ce n’est pas parce qu’un problème n’a pas été résolu qu’il est impossible à résoudre."

Agatha Christie

Conseillez Sciencetips
à vos amis

Bonjour,
Aujourd'hui : "Vieux problème cherche démonstration"
Où l’on se rend compte que les problèmes simples ne sont pas toujours les plus faciles à résoudre.

1742. Pour la centième fois, le mathématicien Euler peste contre son ami et confrère Goldbach.
Il lui a fait parvenir, dans sa dernière lettre, un épineux problème : démontrer une observation a priori extrêmement simple qui est que "tout nombre pair supérieur à 2 peut s’écrire comme la somme de deux nombres premiers".

Simple peut-être, mais ni Goldbach ni Euler n’y parviennent. Pire : 277 ans plus tard, personne n’a encore trouvé la solution.

Vous n'arrivez pas à voir les images ? Contactez-nous sur jean@artips.fr

Jakob Emanuel Handmann, Leonhard Euler, 1756, huile sur toile, Deutsches Museum, Munich
Voir en grand

Pourtant, l’énoncé n’a rien de sorcier. Les nombres pairs, pas de soucis, il s’agit des multiples de 2 : 2, 4, 6, 8…

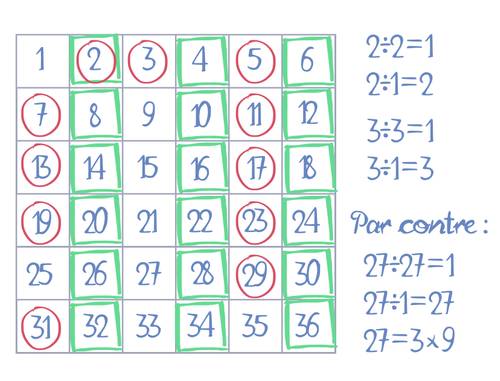
Les nombres premiers, ce sont les nombres entiers qui ne sont divisibles que par 1 ou par eux-mêmes. Par exemple, 27 n’est pas premier, car 3x9=27. En revanche les nombres 2, 3, 5, 7, 11, etc. sont premiers.

En vert : les nombres pairs,
En rouge : les nombres premiers
Illustration Sciencetips
Voir en grand

Lorsque l’on reprend la conjecture (la proposition non démontrée) de Goldbach pour les premiers nombres pairs, c’est facile : 4=2+2, 6=3+3, 8=5+3, 10=5+5 ou 7+3.

Cela fonctionne : ils sont bien la somme de deux nombres premiers, 10 possède même deux combinaisons. Mais qu’en est-il des suivants ?

Illustration Sciencetips
Voir en grand

Pour le savoir, on utilise aujourd’hui des ordinateurs. Grâce à eux, on a pu valider la conjecture jusqu’à plusieurs milliards de milliards. Ce qui laisse supposer que cette dernière est vraie.

Malheureusement, cela ne prouve rien. Eh oui, le nombre suivant pourrait très bien ne pas suivre la règle.

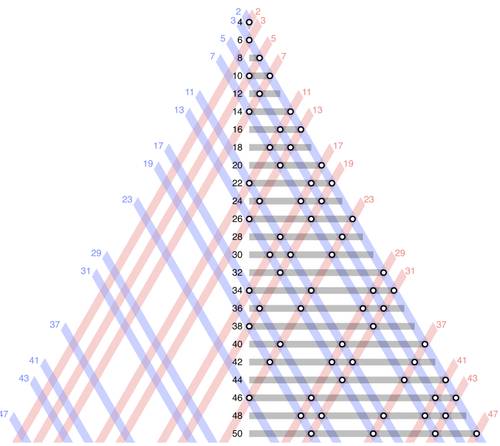
La conjecture de Goldbach sur les nombres pairs de 4 à 50, 2012, illustration, photo : Adam Cunningham, John Ringland
Voir en grand

Et impossible de tester tous les nombres pairs, vu qu’ils sont infinis ! Il est donc nécessaire d’élaborer une démonstration mathématique générale pour montrer qu’elle est vraie. À l’inverse, un seul contre-exemple permettrait de montrer que la conjecture est fausse.

Tentés par l’aventure ? Sachez qu’entre 2000 et 2002, une récompense a été promise à quiconque démontrerait la conjecture de Goldbach. Le montant ? Un million de dollars ! Alors à vos crayons.