De l’eau a coulé sous les ponts !

"Un bon croquis vaut mieux qu’un long discours."

Napoléon

Conseillez Sciencetips
à vos amis

Bonjour,
Aujourd'hui : "De l’eau a coulé sous les ponts !"
Où l’on apprend qu’une promenade peut faire progresser les mathématiques.

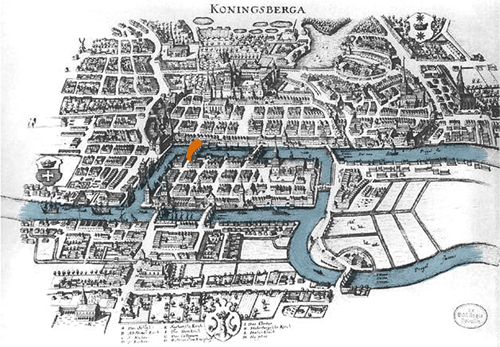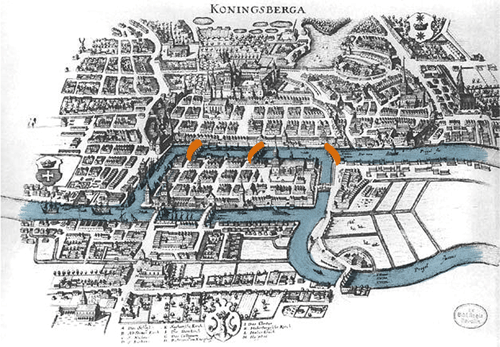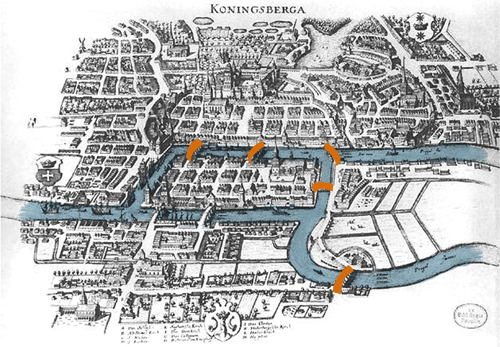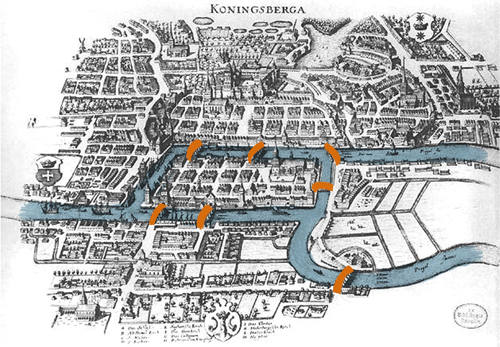
1736, Königsberg (actuelle Russie). Accoudé à l'un des sept ponts de la ville, Leonhard Euler regarde la rivière d'un air songeur. Les habitants viennent de lui poser une colle…

Existe-t-il un chemin permettant de se promener dans toute la ville en ne passant qu’une seule fois par chacun des ponts ?

Vous n'arrivez pas à voir les images ? Contactez-nous sur jean@artips.fr

Illustration Sciencetips
Voir en grand

Bien décidé à résoudre cette énigme, Euler se met au travail. Pour ce faire, le mathématicien saisit une feuille de papier et commence à dessiner un plan de la ville.

Traversée par une rivière, cette dernière est divisée en 4 quartiers (dont 2 îles) tous accessibles via 7 ponts.

Matthäus Merian, Plan de Königsberg, 1651, gravure, photo : Merian-Erben / Illustration Sciencetips
Voir en grand

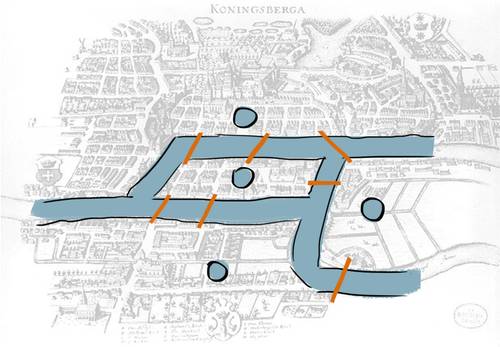
Mais en mathématiques, un pont ou une île ne signifient rien. Euler simplifie donc le problème : il trace des traits à la place des ponts, et les quartiers laissent la place à des points.

La ville de Königsberg est ainsi réduite à un schéma composé de 4 points (ou sommets) et 7 traits (ou arcs).

Illustration Sciencetips
Voir en grand

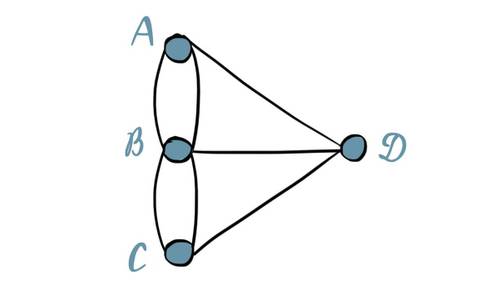
Il vient de réaliser ce que les mathématiciens appellent un "graphe".

Pour résoudre le problème, il suffit de trouver comment relier tous les sommets en ne passant qu’une seule fois par chaque arc. On vous laisse quelques minutes pour essayer de résoudre le problème ?

Illustration Sciencetips
Voir en grand

Après plusieurs essais, Euler tient enfin la solution : c’est impossible ! Les habitants de la ville ne pourront jamais faire une promenade idéale. Il faudrait pour cela un nombre pair d’arcs pour chaque sommet.

Pour faire simple, il faudrait pouvoir arriver par un pont, et repartir par un autre. Euler vient de poser les bases d’une nouvelle branche des mathématiques : la "théorie des graphes".

Jakob Emanuel Handmann, Leonhard Euler, 1753, pastel sur papier, Musée d’art de Bâle, Bâle
Voir en grand

Depuis cette étude, de l’eau a coulé sous les ponts, mais la théorie des graphes reste aujourd’hui extrêmement utile pour étudier les réseaux, et notamment… les réseaux sociaux.

Alors la prochaine fois que vous ajoutez un ami sur Facebook, dites-vous que vous ajoutez un sommet à votre graphe !